在我司光学机械部设计产品的过程中，除了面临常见的产品结构问题外，还需要考虑产品的振动可靠性。由于实验条件限制以及实验成本与周期等因素影响，我司基于有限元技术，采用CAE软件进行数值仿真，通过加载真实的震动条件和颠震条件，对产品进行包括随机振动分析、谐响应分析、瞬态动力学分析等在内的动力响应分析，其结果对产品设计优化具有重要的指导意义。
其中，随机振动分析是基于概率的功率谱密度分析载荷过程中的统计规律，应用于总体上有一定统计规律但不能用确定函数描述的随机振动场景。
表1. 随机振动功率密度谱
| 频率 |
功率谱密度 |
方向 |
| 20~80 |
0.00704 |
X/Y/Z |
| 80~350 |
0.04 |
X/Y/Z |
| 350~2000 |
0.2272 |
X/Y/Z |
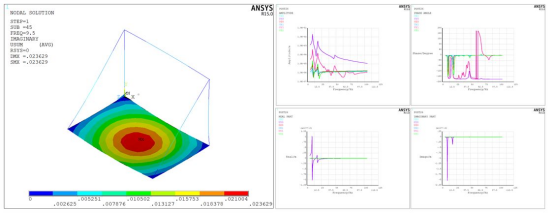
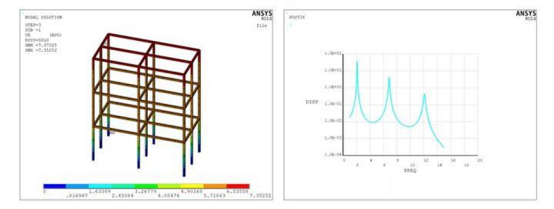图1. 随机振动分析结构位移结果（3σ）
谐响应分析是对线性系统施加一系列不同频率的周期正弦激励，分析其在周期激励下的周期响应情况。通过谐响应分析，可以获取系统在特定周期载荷下所激发的固定频率和薄弱部位，也可以得到整个过程中的结构响应。
表2. 谐响应分析振动条件
| 频率 |
位移幅值 |
加速度幅值 |
| 20~80 |
0.00704 |
X/Y/Z |
| 80~350 |
0.04 |
X/Y/Z |
图2. 谐响应分析结构及采集点位移等结果
瞬态动力学分析是用于确定承认任意的随时间变化载荷结构的动力学响应的一种方法，应用于惯性力和阻尼作用较为重要的、稳态载荷、瞬态载荷和简谐载荷的任意组合作用下的随时间变化的位移、应变、应力及力的分析，得到结构强度和受力比较复杂的受力关系。
表3. 瞬态动力学颠震条件
| 波形 |
重复频率 |
加速度幅值 |
脉冲持续时间 |
总冲击次数 |
| 半正弦波 |
30 r/min |
7 g |
16 ms |
1000 次 |
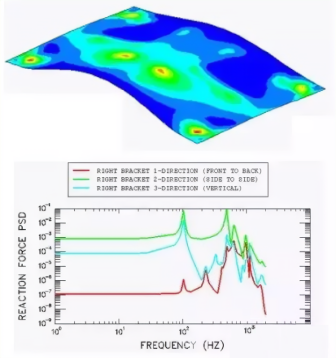图3. 瞬态动力学结构3轴位移结果
作者：胡瑞
2022年1月17日
